Decision Trees Pt. 1
So far, we’ve looked at parametric models. These are models that have set assumptions that are required to make them statistically valid. There are other classes of bad-boy type models that don’t follow the rules, and don’t really care. One of the more popular types that we’ll go over today is the basic decision tree. This lesson is going to cover the basics of a simple decision tree model, but we’ll expand on it much more in the near future.
The Basics of a Decision Tree
A decision tree is a pretty simple model that can be applied to both regression and classification problems. The general idea is that we split up our data on a set variable based on how we can best determine our response, y. The split is determined at each step by what leads to the largest reduction in RSS for regression and the most pure nodes for classification (purity essentially measures our buckets of predictions on their mix of classes; buckets that contain mostly one class are said to be more pure than one that has a mix of multiple classes).
Let’s say we have a binary classification problem; we’re trying to predict whether a team wins or losses a game based on, oh let’s say field goal percentage. The best split of our data to predict y might be 55%, so if a team shot 55% or higher, they’d go down one branch where we would predict that team wins and teams that shot less than 55% would go down the other branch where we would predict they lose. If we stopped it there, we could look at the terminal node, or leaf, and see how right our predictions were.
See where the tree terminology comes from? And we can expand this simple one split model to multiple splits with more than two leaves. We might not want to say all teams that under 55% lose; we could make another split after the first one that separates the data based on whether the team shot above or below 45%. We can also throw in more variables and split on those.
The same general idea can work for regression problems. Everything in each of the terminal nodes would have a prediction based on the mean of the terminal node it ends up in.
Now, before we see an actual example, I want to warn about overfitting opportunities with this model. It’s easy to see that our decision tree could continue to make miniscule splits to our data to the point where we have a crazy amount of branches. We’ll need to prune our tree back, removing branches and using some form of cross validation to determine a good number of splits that doesn’t overfit.
The Data
We’ll be predicting wins by the Pacers in the 2016-17 season similarly
to how we did so in the logistic regression blog. It’ll be a good way to
compare these different methods. We can scrape the data we’ll be using
from basketball-reference. We’ll also split the data into a training and
testing set using createDataPartition() in caret. This method will
allow us to train the model on 70% of our data while using the other 30%
to see how our model reacts to new data. The set.seed() function makes
sure that you get the same split that I do.
library(rvest)
library(caret)
library(dplyr)
pacers<-
"http://www.basketball-reference.com/teams/IND/2017/gamelog/" %>%
read_html('#tgl_basic') %>%
html_table() %>%
#removing the scraped dataframe from a list
.[[1]] %>%
#selecting specific columns
.[,2:23] %>%
#changing column names to names in the first row
`colnames<-` (make.names(.[1,], unique=T)) %>%
#removing excess headers in dataframe
filter(Date!="Date" & Date!="") %>%
rename(H.A=X, Opp.Score=Opp.1) %>%
#creating a home and away column
mutate(H.A=ifelse(H.A=="@", "A", "H")) %>%
#changing variables either to factors or numbers
mutate_at(funs(as.numeric), .vars=vars(Tm:TOV)) %>%
mutate_at(funs(factor), .vars=vars(W.L, H.A))
set.seed(1234)
split<- createDataPartition(y = pacers$W.L, times = 2, p = .7, list = F)
training<- pacers[split,]
testing<- pacers[-split,]
Creating a Tree
Now, we’ll be using the rpart package to develop this decision tree,
so install it and load it into your R session. There are multiple
packages for this though, so if you don’t like rpart explore with some
other options.
The way we’ll develop our decision tree model is through the rpart()
function. We’ll begin by just specifying the model formula, the method,
and the data. The only argument that is new is method; this specifies
whether we want classification or regression trees. We’re using
classification in this case, so we’ll specify method="class". The
default split criteria is the Gini Index which is found by taking the
sum of the squared predicted probabilities and subtracting it from one.
library(rpart)
set.seed(1234)
simple.dt<- rpart(W.L ~ FG. + TRB + H.A + TOV, method="class", data=training)
We can plot our tree by calling plot() on our tree, but this plot can
be a bit cluttered and hard to understand. We can instead use
rpart.plot() from the rpart.plot package to produce a nicer, easier
to understand plot.
library(rpart.plot)
rpart.plot(simple.dt)
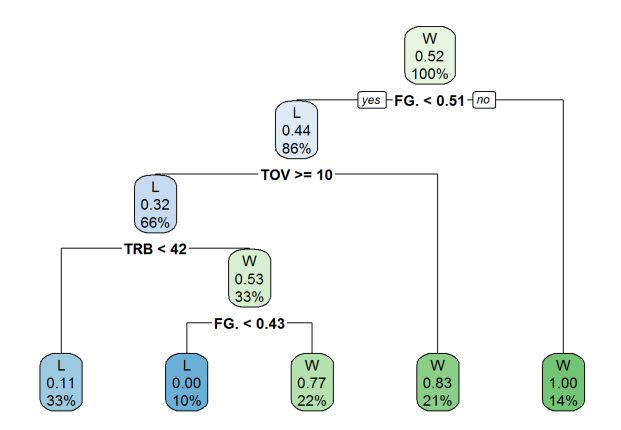
We can see the flow of this decision tree relatively easily. The first node captures all the observations and shows the result, the percentage of said result in the node, and the percentage of observations in the node. So the first node shows win as the output, 52% of all observations in the node are wins, and 100% of the data is included in the node.
The first split is if the Pacers shot less than 51%. If they didn’t, we predict they win. If they did, we move to the next step, which is if they had greater than or equal to 10 turnovers. We move throughout the tree and make predictions this way. We can see at our prediction success at each of the terminal nodes (for example, we were 83% accurate by predicting wins if the team shot less than 51% and had less than 10 turnovers).
Decision trees run the risk of overfitting data as nodes become more and
more distinct. To prevent this, it’s necessary to look at results and
prune back our tree branches. We can look at model results that will
help us gauge overfit by calling the printcp() function. CP is the
complexity parameter and acts as a penalty that controls tree size.
Smaller CP values mean more complex trees (i.e. more splits and terminal
nodes).
printcp(simple.dt)
##
## Classification tree:
## rpart(formula = W.L ~ FG. + TRB + H.A + TOV, data = training,
## method = "class")
##
## Variables actually used in tree construction:
## [1] FG. TOV TRB
##
## Root node error: 56/116 = 0.48276
##
## n= 116
##
## CP nsplit rel error xerror xstd
## 1 0.250 0 1.00 1.14286 0.095648
## 2 0.125 2 0.50 0.71429 0.091415
## 3 0.010 4 0.25 0.37500 0.074055
rpart automatically stops splitting the tree if the fit does not
improve by the CP value in an effort to save computing time. This, along
with several other parameters (such as minimum number of observations
needed for a split, number of cross validation folds, etc.), can be
edited within the rpart.control() function. If you wanted a full tree,
we would simply set cp=0.
We can see the root node error is about 48%; this indicates that
initially predicting all observations as wins would give us about 52%
accuracy. We can see that each CP value has a certain number of splits
as well as rel error, xerror, and xstd values associated with
them. rel error is the training error rate at each level. xerror is
testing error rate developed by cross validation that goes on within
rpart (default is 10 fold cross validation). These error numbers are in
relation to the root node error; so when nsplit is 0, our rel error
is 100% of the root node error. When we perform 2 splits, our
rel error is 50%, or half of the root node error (i.e. around 24%).
There are two general rules of thumb when trying to prune our tree:
-
Choose the split that has the lowest cross validation error
-
Choose the split that is the lowest and within one
xstd(standard deviation) from the lowest cross validation error value.
I would usually go with the second option to try and make sure our tree
doesn’t overfit. In this case, the model with 4 splits has the lowest
xerror, and no simpler model is within one standard deviation of this
xerror value (.375 + .074), so we’ll continue without doing any
pruning. If we wanted to prune back the tree, we could use the
prune.rpart() function to cut the tree at a specific CP value.
Now we can easily predict on our test data set using the predict()
function. We can specify type="class" to get back class predictions.
If we don’t specify this, predictions will come back as predicted
probabilities for each outcome.
test.predictions<- predict(simple.dt, newdata=testing, type="class")
confusionMatrix(test.predictions, testing$W.L, positive = "W")
## Confusion Matrix and Statistics
##
## Reference
## Prediction L W
## L 3 1
## W 2 6
##
## Accuracy : 0.75
## 95% CI : (0.4281, 0.9451)
## No Information Rate : 0.5833
## P-Value [Acc > NIR] : 0.1916
##
## Kappa : 0.4706
## Mcnemar's Test P-Value : 1.0000
##
## Sensitivity : 0.8571
## Specificity : 0.6000
## Pos Pred Value : 0.7500
## Neg Pred Value : 0.7500
## Prevalence : 0.5833
## Detection Rate : 0.5000
## Detection Prevalence : 0.6667
## Balanced Accuracy : 0.7286
##
## 'Positive' Class : W
##
We can see that our overall test set accuracy is 75%. The model predicts wins a bit better than losses, as seen in the sensitivity and specificity values, but this may be a result of the small testing dataset we’re working with in this example.
The main pro of decision trees are that they are easy to visualize and
understand and can be applied to both regression and classification
problems. They are, however, lazy learners. They can give good results,
but a lot of the time, they don’t improve much beyond random guessing.
We can improve them though, through combining several of them together.
The next tutorial will go over a combining method called bagging and
will take a look at the randomforest package.
