The past two tutorials have focused on different models involving a tree-based structure. The last one gave an introduction to the idea of ensemble modeling, or combining multiple models together to get a better prediction. This lesson focuses on a different type of ensemble model called boosting.

The previous ensemble model we went over was bagging, in which we create many separate models based on different samples of data from which we get a combined output. Boosting does create multiple models, but they aren’t all independent like in the bagging process; boosting adds models sequentially based on the errors of previous models. Essentially, we have a model that’s learning from its own mistakes!

Data

We’ll be using the same dataset we used from the bagging tutorial to learn a bit more about boosting. We’ll be trying to predict whether certain shots are made or missed based on a bunch of different factors about the shot. The data can be downloaded from this link and can then be loaded into the global environment; note that the location you load it from depends on where you saved the data.

#Remember to specify where  YOU saved it in your directory!

shot_log<- read.csv("~/R/blog/January 2018/shot log.csv")

Boosting

So boosting is a pretty complicated subject, so be prepared for me to rant a bit before I get into actually implementing it in R! The down and dirty of it, though, is that we are building multiple weak learners sequentially, based off of the shortcomings of the previous model in the chain. These models are then summed together to create a strong, ensemble model.

Remember that a weak learner is a model that does only slightly better at making predictions than random guessing. The idea is that if you add a bunch of weak learners together, then you’ll get a strong model!

Adaptive Boosting (AdaBoost)

AdaBoost was the first real version of boosting. We aren’t going to go over using it in R, but I wanted to present the idea so we could compare it to a more evolved version of boosting that we will be coding.

Adaboost learns from its mistakes by looking at misclassified predictions. Each model added tries to focus on improving the misclassifications of the previous model. How does it do this? By applying weights to the training observations; each time a new model is built, weights are calculated so that misclassified observations weigh more heavily. The new weak learner will focus its efforts on trying to correctly predict higher weighted samples.

The final ensemble model is the weighted sum of all of the weak learners developed. Each weak learner is given a weight based on its prediction accuracy; so models that were better at making predictions have higher weights in the final model.

Gradient Boosted Machines (GBM)

Now, with that short overview of AdaBoost out of the way, let’s get into boosting’s evolved state. GBMs follow the same general boosting idea that AdaBoost developed, but go about it slightly different.

In AdaBoost, we based the new sequential weak learners on misclassified observations; in GBMs, we base new sequential weak learners on the negative gradient of the loss function. Woah, that sounds complicated… let’s take this one step at a time.

Let’s first talk about the loss function. This is a function we are trying to minimize by selecting the best model parameters. This may sound weird or advanced, but it’s a part of modeling in general. Think back again to linear regression; the method we used was ordinary least squares or OLS. OLS was trying to find the best model parameters (coefficients) to minimize the squared residuals. There are several loss functions that can be applied by different models, but the idea is the same: we are trying to minimize said loss function.

Now let’s talk about gradient descent. Imagine we’re at the top of a hill and we want to get to the bottom. Each step we take gets us closer to our overall goal! Gradient descent’s implementation in GBM works in a similar way. The minimum loss function is represented by the bottom of the hill, our ultimate destination. Each additional model sort of acts as a step down the hill towards the optimum minimized value of the loss function.

GBM Parameters

Now that we have an idea of the goal of GBMs, let’s look at some of the more important parameters that go with it.

Two parameters that go hand-in-hand are the number of trees and the learn rate. Lower learn rates require more trees, and higher learn rates require less trees. The number of trees is pretty straightforward; it’s just the amount of tree models we’ll be using. The learn rate is a little more complicated, though. Remember that we are adding models sequentially. The learn rate acts as a weight for each model output so that no one model holds too much influence on the entire ensemble. Now usually, this weight is pretty small (below .1), which requires a fair amount of trees to be built.

You might be asking yourself, “Why are you trying to make this so complicated?” but I have good reason. By using a small learning rate with many trees, we get a more precise idea for an optimal model. I like this cross validated explanation of the topic. As I’ve already mentioned, we’re trying to minimize a loss function, but we want to do so without overfitting. Having a high learning rate would help us reach a perfect model more quickly, but said perfect model is going to be overfit to the training data. We can prevent it from overfitting by tuning back the number of trees, but there’s going to still be space to improve the model without overfitting. Having a lower learning rate allows us to exploit this space.

Going back to the hill example, learning rate is sort of like the step size as we go down the hill. Lower learn rates are smaller steps. We could take larger steps and get to the bottom of the hill faster, but then we’d probably end up overfitting. No, we want a primo spot on the side of the hill, close to the bottom, but not right there; somewhere we might have over-stepped and completely missed had our step size been larger; somewhere that requires taking small steps and a bit of time to get to.

Other parameters that’ll come up that we should think about involve specifics about each tree. Max depth is the number of splits for each tree; again, boosting methods usually keep this number a bit lower to prevent overfitting. The minimum number of observations in each node is the smallest amount of observations for each leaf or terminal node of a tree.

I know GBMs are a pretty heavy topic, but now we have a basic idea of what they do and what goes into them! Let’s jump into applying them with R.

GBM in R

So the first step is to install the gbm package; I already have it installed, so I’m just going to bring it up with the library() function.

library(gbm)

We’ll be using the gbm() function to create our model. If we want to create a classification model (which in this case, we do), we have to input the response variable as numeric. So instead of inputting shot result as made or missed, we’ll input it as 1 and 0. Let’s create a new column called SHOT_RESULT_NUM that takes care of this for us.

library(dplyr)

shot_log<-
  shot_log %>%
  #releveling the factor so the first level is missed and second is made
  mutate(SHOT_RESULT = relevel(SHOT_RESULT, "missed")) %>%
  #taking the numeric version of the factor (which is 1 for
  #missed and 2 for made) and subtracting one, so it's now
  #treated as 0 for missed and 1 for made
  mutate(SHOT_RESULT_NUM = as.numeric(SHOT_RESULT)-1)

Now we’ll split our dataset into a training and testing set, using a 75/25 partition.

library(caret)

set.seed(1234)
#75/25 training testing split
sl_split<- createDataPartition(shot_log$SHOT_RESULT, p=.75, list=F)

training<- shot_log[sl_split, ]
testing<- shot_log[-sl_split, ]

Now we’ll create a GBM model using the gbm() function. We’ll also add in some specific parameters and go over what each means (I’ve gone over all of the parameters we’ll specify, but the terminology for some are slightly different). We’ll be using the same variables used in the bagging lesson to predict the result of a shot.

set.seed(1234)
gbm.model<- gbm(SHOT_RESULT_NUM ~ LOCATION + PERIOD + SHOT_CLOCK + DRIBBLES 
                + TOUCH_TIME + SHOT_DIST + CLOSE_DEF_DIST, 
                data=training, n.trees = 500, interaction.depth = 3,
                n.minobsinnode = 25, shrinkage = .01)

## Distribution not specified, assuming bernoulli ...

summary(gbm.model) #look at model output

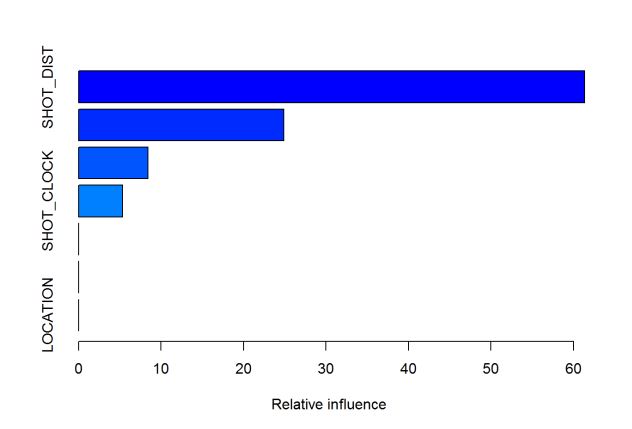
##                           var     rel.inf
## SHOT_DIST           SHOT_DIST 61.34414401
## CLOSE_DEF_DIST CLOSE_DEF_DIST 24.89662478
## TOUCH_TIME         TOUCH_TIME  8.39940483
## SHOT_CLOCK         SHOT_CLOCK  5.32791644
## DRIBBLES             DRIBBLES  0.02277907
## PERIOD                 PERIOD  0.00913088
## LOCATION             LOCATION  0.00000000

So we created a GBM model with 500 trees. The learning rate, represented by shrinkage is set to .01. The number of splits in each tree is 3, represented by interaction.depth, and the minimum observations in each terminal node is set to 25.

By calling summary on the model, we get a measure of importance for each variable. This number represents the relative influence each variable has on reducing the loss function, so higher values indicate more important variables. In this case, the two most important variables were the distance of the shot as well as the distance of the closest defender.

Now let’s look at the predictions. To get predicted probabilities of the positive class (in this case, probability of making a shot), specify type = "response". We also need to specify the number of trees used in the model; this number is stored in the model object if you don’t want to type it out.

We’ll store test set predictions in the object gbm.pred. These predictions are rounded so the actual class predictions are stored (1 or 0). The confusionMatrix function from caret is used to create a confusion matrix; the positive class is specified as 1 or made shot.

gbm.pred<- round(predict(gbm.model, n.trees = gbm.model$n.trees, 
                 type = "response", newdata = testing), 0)

confusionMatrix(gbm.pred, testing$SHOT_RESULT_NUM, positive = "1")

## Confusion Matrix and Statistics
## 
##           Reference
## Prediction     0     1
##          0 15048  9575
##          1  2493  4901
##                                           
##                Accuracy : 0.6231          
##                  95% CI : (0.6177, 0.6284)
##     No Information Rate : 0.5479          
##     P-Value [Acc > NIR] : < 2.2e-16       
##                                           
##                   Kappa : 0.2052          
##  Mcnemar's Test P-Value : < 2.2e-16       
##                                           
##             Sensitivity : 0.3386          
##             Specificity : 0.8579          
##          Pos Pred Value : 0.6628          
##          Neg Pred Value : 0.6111          
##              Prevalence : 0.4521          
##          Detection Rate : 0.1531          
##    Detection Prevalence : 0.2309          
##       Balanced Accuracy : 0.5982          
##                                           
##        'Positive' Class : 1               
## 

The overall test set accuracy is around 62%, but the model performs much better in predicting missed shots than made shots. We might try and adjusting parameters or resampling the data to get a balanced dataset (stay tuned for a lesson on this).

Now GBMs have a fair amount of interacting parameters that need to be adjusted. One could try and constantly update the model manually, but there are more efficient methods using the caret package to search for optimal model parameters. Next lesson will go over this method and can be applied to any model in the caret package. But for now, we’ll leave it at this.

Conclusion

Boosting provides a new framework for developing ensemble tree models. With this tutorial, we’ll conclude the saga of decision trees. GBMs are the most complicated tree-based model we’ve looked at, but they are also the most powerful. Understanding gradient boosting and not just thinking of it as a black-box method will help you build more powerful models.