With linear regression under our belt, we have a method to predict a numeric dependent variable. But what if the response isn’t numeric? If this is the case, you need to start playing around with classification. Logistic regression is one of the more basic forms of classification. It is used for binary predictions (i.e. two class responses like yes/no), predicting the probability of an observation being a certain class. We’ll explore logistic regression today by trying to predict whether a team wins or loses a game based on different box score statistics.

Data

For this tutorial, we are going to try and predict the outcome of games the Pacers played in the 2016-17 season. I’ll try and hide any dissapointment from the Paul George trade. If I start sounding depressed just remind me that I get to watch Lance Stephenson be our starting point guard next season (tanking with style!). Anyway, we’ll be scraping this data from basketball reference.

library(dplyr)
library(rvest)

pacers<-
  "http://www.basketball-reference.com/teams/IND/2017/gamelog/" %>%
  read_html('#tgl_basic') %>%
  html_table() %>%
  #removing the scraped dataframe from a list
  .[[1]] %>%
  #selecting specific columns
  .[,2:23] %>%
  #changing column names to names in the first row
  `colnames<-` (make.names(.[1,], unique=T)) %>%
  #removing excess headers in dataframe
  filter(Date!="Date" & Date!="") %>%
  rename(H.A=X, Opp.Score=Opp.1) %>%
  #creating a home and away column
  mutate(H.A=ifelse(H.A=="@", "A", "H")) %>%
  mutate_at(funs(as.numeric), .vars=vars(Tm:TOV)) %>%
  mutate_at(funs(factor), .vars=vars(W.L, H.A))

Now if you just looked at the scraped data, you’d get a pretty dirty result. First off, the data is stored in a list, which we removed and put in a dataframe for easier access. Basketball reference also includes opponent stats in their game logs. This could be helpful, but for simplicity, we’ll look at just Pacer stats. This does create an issue with column names. The game logs in basketball reference have two rows of column names, the first specifying team or opponent and the second being the actual stats. R reads the first row as the column names, while inserting the second into the dataframe itself. To get around this, we can simply assign the first row of data to the colnames.

Other issues that we cleaned up were removing the excess headers basketball reference uses every 20 rows, renaming a few columns, and changing up the home or away column which originally specified the home games by leaving a blank. Finally, columns that we wanted to treat as numeric or factors were changed from their current character state.

With a clean dataframe, we can start getting into the fun stuff.

Understanding Logistic Regression

Looking at our data, we have a lot of statistics that could influence whether the Pacers win or lose. To make it simple, let’s choose only a few to look at. Looking over the stats, I chose FG%, total rebounds, home or away, and turnovers as columns we’ll use as predictors. W.L is the result of the game and will be our dependent variable.

pacers<- 
  pacers %>%
  select(W.L, FG., TRB, H.A, TOV)

head(pacers)

##   W.L   FG. TRB H.A TOV
## 1   W 0.505  52   H  16
## 2   L 0.378  49   A  13
## 3   L 0.489  33   A  13
## 4   W 0.471  43   H  15
## 5   L 0.469  32   A  21
## 6   W 0.535  36   H  11

Let’s look at a scatter plot of field goal % against the games result.

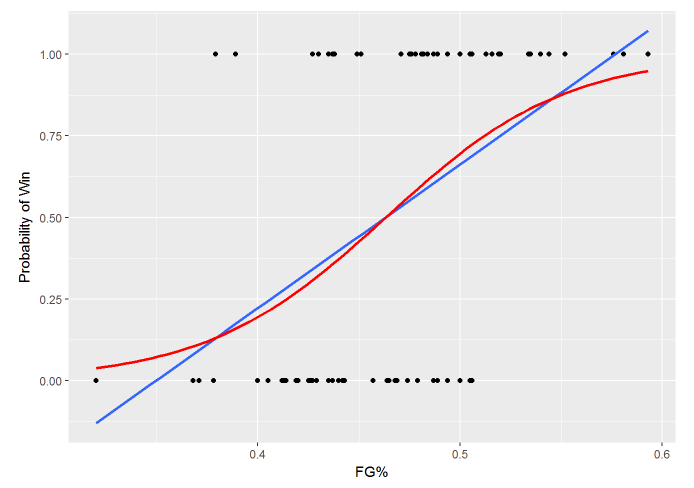
The y-value is the probability of a win. A linear regression line is shown in blue while a logistic line is shown in red. We can see that the linear line goes beyond 1 and 0 and isn’t very flexible. It doesn’t make much sense to have probabilities that are over 1 or negative. The logistic line is s-shaped and bound between 1 and 0, making it better for a binary problem like this.

Logistic regression uses the logistic function to find the probability of the positive class in the dependent variable (in this example, Win). The logistic function looks like:

Probability(Y) = e^(B0 + B1X) / 1 + e^(B0 + B1X)

Remember from the linear regression that B0 is the intercept term and Bi (in this case B1) is the coefficient for the predictor.

The odds of an event is the events probability of happening divided by the probability of it not happening. So if there was an 80% chance of the Pacers winning a game, their odds would be .8 / 1-.8 or 4 to 1. Think of this game being played 5 times; the odds say the Pacers would win 4 times compared to 1 loss. The logistic equation can be manipulated to give us the odds like so:

Probability(Y) / (1 - Probability(Y)) = e^(B0 + B1X)

Now if we take the logarithm of both sides we get:

log(Probability(Y) / (1 - Probability(Y))) = B0 + B1X

The left hand side of the equation is called the log odds. We can see that the right side now looks like the formula we used in linear regression! The log odds are linear; a one unit increase in X would lead to an increase (or decrease depending on the coefficient B1) of B1 to the log odds. This is similar to how a one unit increase in X leads to an increase or decrease in Y of B1 in linear regression. Remember, the change in X changes the LOG ODDS by the value of B1, NOT the probability.

Performing Logistic Regression

In the linear regression tutorial, we used lm to develop a model. For logistic regression, we are going to use glm. glm stands for generalized linear model and can fit several different families of linear models, including logistic. Here, we’ll fit a model predicting W.L with all of our predictors. You can write each predictor out, like we did in the linear regression tutorial, or you can just use a . to tell R we want all predictors included.

set.seed(1234)
pacers.glm<- glm(W.L ~ ., data=pacers, family=binomial)

The command is similar to lm, except that we need to define the family command, which we specify as binomial, indicating logistic regression. We can use summary to look at the general output of our model.

summary(pacers.glm)

## 
## Call:
## glm(formula = W.L ~ ., family = binomial, data = pacers)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -1.8954  -0.6090   0.1407   0.5709   2.4511  
## 
## Coefficients:
##              Estimate Std. Error z value Pr(>|z|)    
## (Intercept) -25.28876    6.34006  -3.989 6.64e-05 ***
## FG.          34.37660    9.30910   3.693 0.000222 ***
## TRB           0.24763    0.06854   3.613 0.000303 ***
## H.AH          1.43891    0.64625   2.227 0.025977 *  
## TOV          -0.12941    0.09874  -1.311 0.189971    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 113.627  on 81  degrees of freedom
## Residual deviance:  66.142  on 77  degrees of freedom
## AIC: 76.142
## 
## Number of Fisher Scoring iterations: 5

Here we get an output similar to the output of lm. It appears as though field goal percentage, total rebounds, and the game being at home all are significant based on their p-values. All three of these variables have a positive coefficient estimate, indicating that higher field goal percentages and total rebound numbers, as well as the game being home rather than away increase the log odds of a Pacers win. Number of turnovers has a negative relationship with the log odds of a Pacers win, but is not significant. The regression equation would look like this:

log odds(Win) = -25.28 + 34.37(FG.) + .24(TRB) + 1.43(H.A) -.12(TOV)

The deviance is a measure of fit for the model. The null deviance is the deviance of the model with only the intercept while the residual deviance is the deviance of the model with all of our predictors. We want our residual deviance to be lower than the null (while also not sacrificing a ton of degrees of freedom). Here, our residual deviance is significantly lower than the null while only sacrificing 4 degrees of freedom, indicating that this model is better than simply making predictions with the intercept.

Another, more straightforward way of assessing the model is by checking the accuracy of predictions. Let’s start by using the predict function on our model. We need to specify type = "response" to predict probabilities rather than log odds.

pacer.prediction<- predict(pacers.glm, type="response")

head(pacer.prediction)

##          1          2          3          4          5          6 
## 0.98682737 0.13669425 0.12033458 0.74045082 0.01871131 0.88418547

Now, because probabilities were predicted and not classes, we need to set a probability threshold of what is considered a predicted win and loss. Here, we’ll just say that .5 and above is a win. There could be a scenario where you might want to change this up, but this seems like a generally accepted cutoff.

pacer.prediction<- factor(ifelse(pacer.prediction>=.5, "W", "L"))

head(pacer.prediction)

## 1 2 3 4 5 6 
## W L L W L W 
## Levels: L W

We can now compare this vector of predictions to the actual values:

mean(pacer.prediction==pacers$W.L)

## [1] 0.7926829

Overall, our accuracy is close to 80%. We would want to measure our accuracy on observations we didn’t train the model on (a form of cross-validation), but I’ll save that for a future tutorial.

With a good idea of the logistic regression process, we can now venture into the world of classification. Whether this is predicting a game result, or a shot result, it opens up a lot more ideas of how to implement statistics in a basketball frame of mind.